Python, MATLAB, Julia, R code: Chapter 7
Acknowledgement: The Julia code is written by the contributors listed here.
Acknowledgement: The R code is written by contributors listed here.
Chapter 7.1 Principles of Regression
Linear regression: Straight Line
# MATLAB code to fit data points using a straight line
N = 50;
x = rand(N,1)*1;
a = 2.5; % true parameter
b = 1.3; % true parameter
y = a*x + b + 0.2*rand(size(x)); % Synthesize training data
X = [x(:) ones(N,1)]; % construct the X matrix
theta = X\y(:); % solve y = X theta
t = linspace(0, 1, 200); % interpolate and plot
yhat = theta(1)*t + theta(2);
plot(x,y,'o','LineWidth',2); hold on;
plot(t,yhat,'r','LineWidth',4);
# Python code to fit data points using a straight line import numpy as np import matplotlib.pyplot as plt N = 50 x = np.random.rand(N) a = 2.5 # true parameter b = 1.3 # true parameter y = a*x + b + 0.2*np.random.randn(N) # Synthesize training data X = np.column_stack((x, np.ones(N))) # construct the X matrix theta = np.linalg.lstsq(X, y, rcond=None)[0] # solve y = X theta t = np.linspace(0,1,200) # interpolate and plot yhat = theta[0]*t + theta[1] plt.plot(x,y,'o') plt.plot(t,yhat,'r',linewidth=4)
# Julia code to fit data points using a straight line N = 50 x = rand(N) a = 2.5 # true parameter b = 1.3 # true parameter y = a*x .+ b + 0.2*rand(N) # Synthesize training data X = [x ones(N)] # construct the X matrix theta = X\y # solve y = X*theta t = range(0,stop=1,length=200) yhat = theta[1]*t .+ theta[2] # fitted values at t p1 = scatter(x,y,makershape=:circle,label="data",legend=:topleft) plot!(t,yhat,linecolor=:red,linewidth=4,label="best fit") display(p1)
# R code to fit data points using a straight line library(pracma) N <- 50 x <- runif(N) a <- 2.5 # true parameter b <- 1.3 # true parameter y <- a*x + b + 0.2*rnorm(N) # Synthesize training data X <- cbind(x, rep(1, N)) theta <- lsfit(X, y)$coefficients t <- linspace(0, 1, 200) yhat <- theta[2]*t + theta[1] plot(x, y, pch=19) lines(t, yhat, col='red', lwd=4) legend("bottomright", c("Best Fit", "Data"), fill=c("red", "black"))
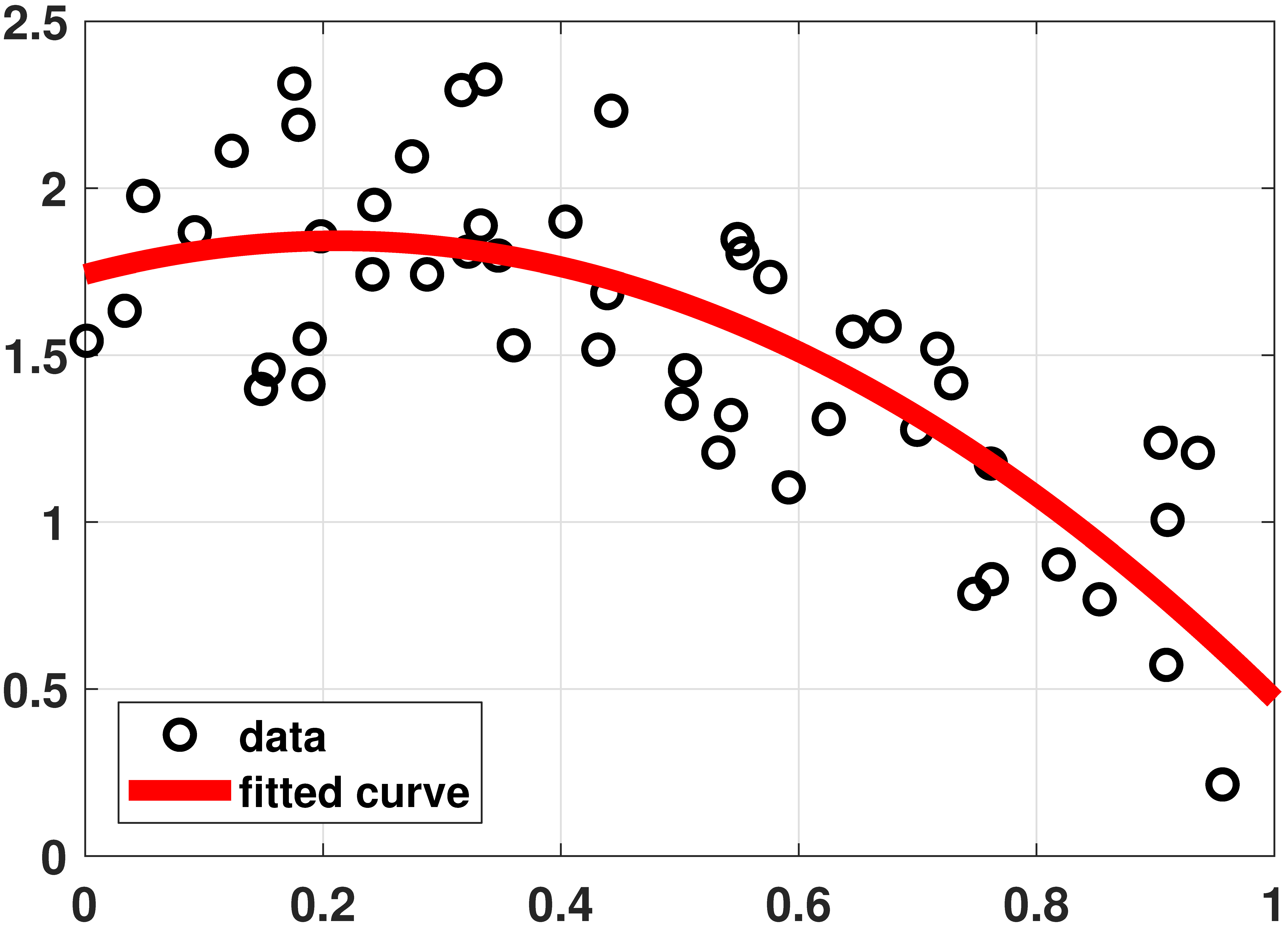
Linear regression: Polynomial
% MATLAB code to fit data using a quadratic equation N = 50; x = rand(N,1)*1; a = -2.5; b = 1.3; c = 1.2; y = a*x.^2 + b*x + c + 1*rand(size(x)); N = length(x); X = [ones(N,1) x(:) x(:).^2]; beta = X\y(:); t = linspace(0, 1, 200); yhat = theta(3)*t.^2 + theta(2)*t + theta(1); plot(x,y, 'o','LineWidth',2); hold on; plot(t,yhat,'r','LineWidth',6);
# Python code to fit data using a quadratic equation
import numpy as np
import matplotlib.pyplot as plt
N = 50
x = np.random.rand(N)
a = -2.5
b = 1.3
c = 1.2
y = a*x**2 + b*x + c + 0.2*np.random.randn(N)
X = np.column_stack((np.ones(N), x, x**2))
theta = np.linalg.lstsq(X, y, rcond=None)[0]
t = np.linspace(0,1,200)
yhat = theta[0] + theta[1]*t + theta[2]*t**2
plt.plot(x,y,'o')
plt.plot(t,yhat,'r',linewidth=4)
# Julia code to fit data using a quadratic equation N = 50 x = rand(N) a = -2.5 b = 1.3 c = 1.2 X = x.^[0 1 2] #same as [ones(N) x x.^2] y = X*[c,b,a] + rand(N) theta = X\y t = range(0,stop=1,length=200) yhat = (t.^[0 1 2])*theta #same as (t.^collect(0:2)')*theta p2 = scatter(x,y,makershape=:circle,label="data",legend=:bottomleft) plot!(t,yhat,linecolor=:red,linewidth=4,label="fitted curve") display(p2)
# R code to fit data using a quadratic equation
N <- 50
x <- runif(N)
a <- -2.5
b <- 1.3
c <- 1.2
y <- a*x**2 + b*x + c + 0.2*rnorm(N)
X <- cbind(rep(1, N), x, x**2)
theta <- lsfit(X, y)$coefficients
t = linspace(0, 1, 200)
print(theta)
yhat = theta[1] + theta[2]*t + theta[3]*t**2
plot(x,y,pch=19)
lines(t,yhat,col='red',lwd=4)
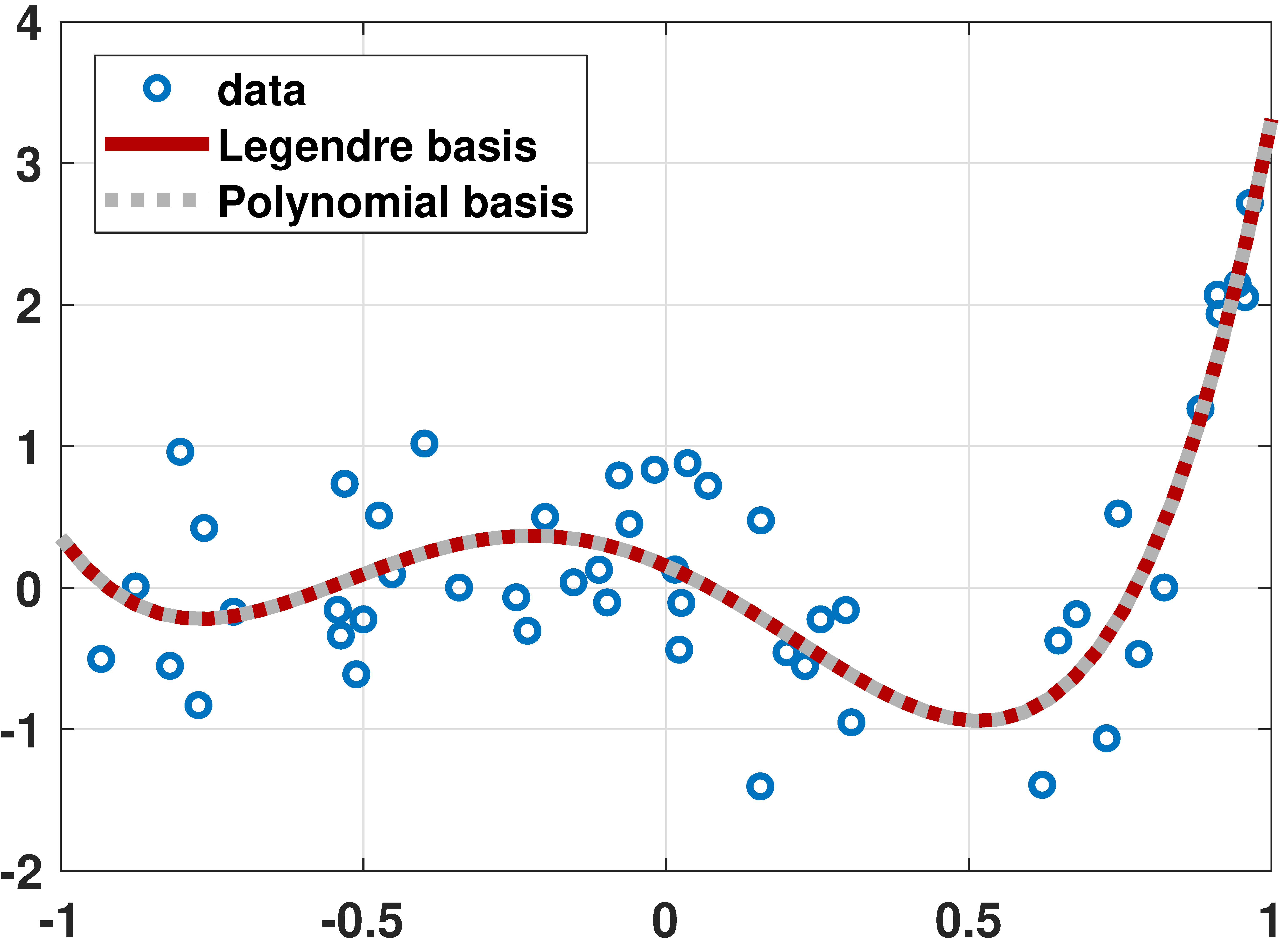
Legendre Polynomial
% MATLAB code to fit data using Legendre polynomials
N = 50;
x = 1*(rand(N,1)*2-1);
a = [-0.001 0.01 +0.55 1.5 1.2];
y = a(1)*legendreP(0,x) + a(2)*legendreP(1,x) + ...
+ a(3)*legendreP(2,x) + a(4)*legendreP(3,x) + ...
+ a(5)*legendreP(4,x) + 0.5*randn(N,1);
X = [legendreP(0,x(:)) legendreP(1,x(:)) ...
legendreP(2,x(:)) legendreP(3,x(:)) ...
legendreP(4,x(:))];
beta = X\y(:);
t = linspace(-1, 1, 200);
yhat = beta(1)*legendreP(0,t) + beta(2)*legendreP(1,t) + ...
+ beta(3)*legendreP(2,t) + beta(4)*legendreP(3,t) + ...
+ beta(5)*legendreP(4,t);
plot(x,y,'ko','LineWidth',2,'MarkerSize',10); hold on;
plot(t,yhat,'LineWidth',6,'Color',[0.9 0 0]);
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import eval_legendre
N = 50
x = np.linspace(-1,1,N)
a = np.array([-0.001, 0.01, 0.55, 1.5, 1.2])
y = a[0]*eval_legendre(0,x) + a[1]*eval_legendre(1,x) + \
a[2]*eval_legendre(2,x) + a[3]*eval_legendre(3,x) + \
a[4]*eval_legendre(4,x) + 0.2*np.random.randn(N)
X = np.column_stack((eval_legendre(0,x), eval_legendre(1,x), \
eval_legendre(2,x), eval_legendre(3,x), \
eval_legendre(4,x)))
theta = np.linalg.lstsq(X, y, rcond=None)[0]
t = np.linspace(-1, 1, 50);
yhat = theta[0]*eval_legendre(0,t) + theta[1]*eval_legendre(1,t) + \
theta[2]*eval_legendre(2,t) + theta[3]*eval_legendre(3,t) + \
theta[4]*eval_legendre(4,t)
plt.plot(x,y,'o',markersize=12)
plt.plot(t,yhat, linewidth=8)
plt.show()
# Julia code to fit data using Legendre polynomials using LegendrePolynomials N = 50 x = rand(N)*2 .- 1 a = [-0.001, 0.01, 0.55, 1.5, 1.2] X = hcat([Pl.(x,p) for p=0:4]...) # same as [Pl.(x,0) Pl.(x,1) Pl.(x,2) Pl.(x,3) Pl.(x,4)] y = X*a + 0.5*randn(N) theta = X\y t = range(-1,stop=1,length=200) yhat = hcat([Pl.(t,p) for p=0:4]...)*theta p3 = scatter(x,y,makershape=:circle,label="data",legend=:bottomleft) plot!(t,yhat,linecolor=:red,linewidth=4,label="fitted curve") display(p3)
# R code to fit data using Legendre polynomials library(pracma) N <- 50 x <- linspace(-1,1,N) a <- c(-0.001, 0.01, 0.55, 1.5, 1.2) y <- a[1]*legendre(0, x) + a[2]*legendre(1, x)[1,] + a[3]*legendre(2, x)[1,] + a[4]*legendre(3, x)[1,] + a[5]*legendre(4, x)[1,] + 0.2*rnorm(N) X <- cbind(legendre(0, x), legendre(1, x)[1,], legendre(2, x)[1,], legendre(3, x)[1,], legendre(4, x)[1,]) # good beta <- mldivide(X, y) t <- linspace(-1, 1, 50) yhat <- beta[1]*legendre(0, x) + beta[2]*legendre(1, x)[1,] + beta[3]*legendre(2, x)[1,] + beta[4]*legendre(3, x)[1,] + beta[5]*legendre(4, x)[1,] plot(x, y, pch=19, col="blue") lines(t, yhat, lwd=2, col="orange")
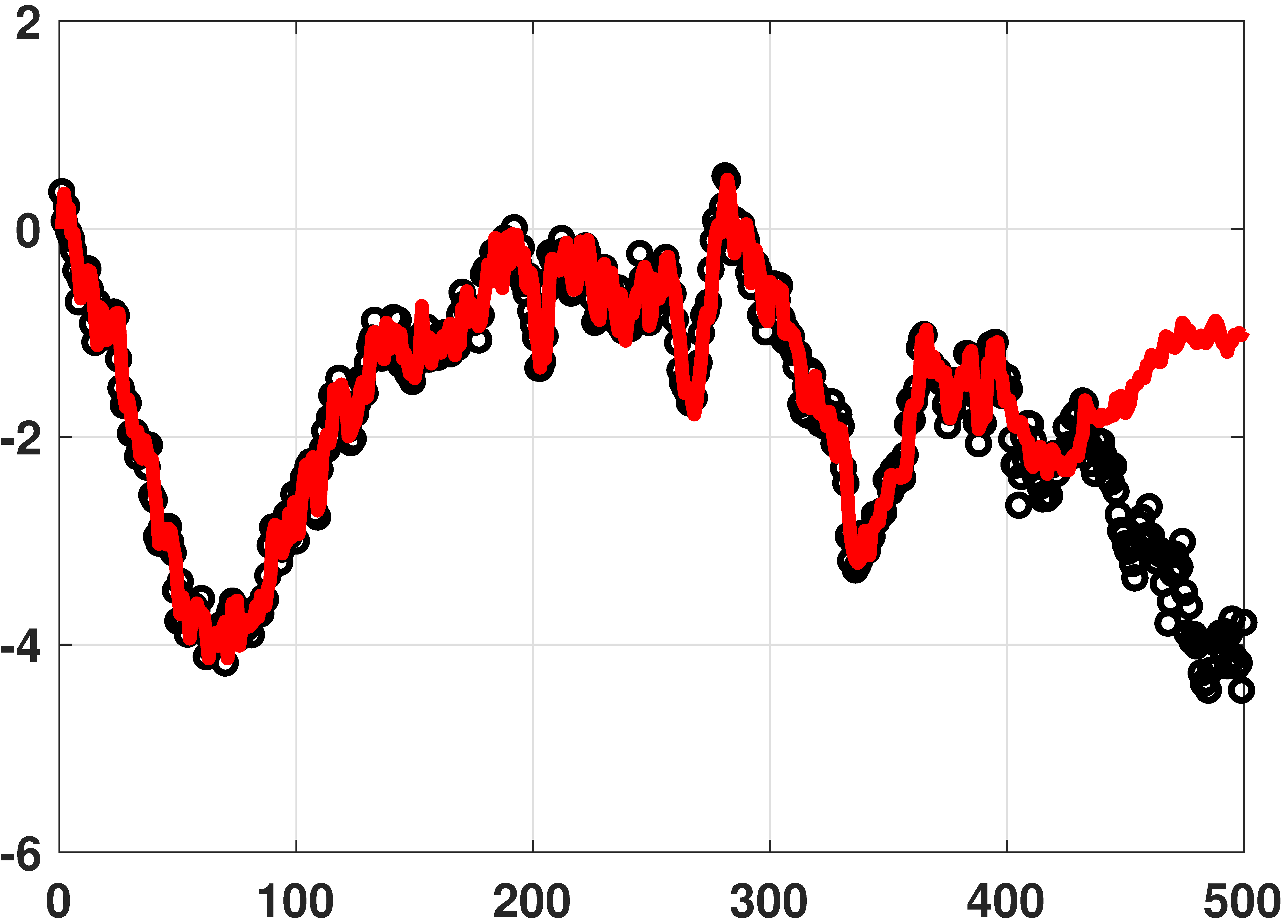
Auto-regressive model
% MATLAB code for auto-regressive model N = 500; y = cumsum(0.2*randn(N,1)) + 0.05*randn(N,1); % generate data L = 100; % use previous 100 samples c = [0; y(1:400-1)]; r = zeros(1,L); X = toeplitz(c,r); % Toeplitz matrix theta = X\y(1:400); % solve y = X theta yhat = X*theta; % prediction plot(y(1:400), 'ko','LineWidth',2);hold on; plot(yhat(1:400),'r','LineWidth',4);
# Python code for auto-regressive model
import numpy as np
import matplotlib.pyplot as plt
from scipy.linalg import toeplitz
N = 500
y = np.cumsum(0.2*np.random.randn(N)) + 0.05*np.random.randn(N)
L = 100
c = np.hstack((0, y[0:400-1]))
r = np.zeros(L)
X = toeplitz(c,r)
theta = np.linalg.lstsq(X, y[0:400], rcond=None)[0]
yhat = np.dot(X, theta)
plt.plot(y[0:400], 'o')
plt.plot(yhat[0:400],linewidth=4)
# Julia code for auto-regressive model using ToeplitzMatrices N = 500 y = cumsum(0.2*randn(N)) + 0.05*randn(N) # generate data L = 100 # use previous 100 samples c = [0; y[1:400-1]] r = zeros(L) X = Matrix(Toeplitz(c,r)) # Toeplitz matrix, converted theta = X\y[1:400] # solve y = X*theta yhat = X*theta # prediction p4 = scatter(y[1:400],makershape=:circle,label="data",legend=:bottomleft) plot!(yhat[1:400],linecolor=:red,linewidth=4,label="fitted curve") display(p4)
# R code for auto-regressive model
library(pracma)
N <- 500
y <- cumsum(0.2*rnorm(N)) + 0.05*rnorm(N)
L <- 100
c <- c(0, y[0:(400-1)])
r = rep(0, L)
X = Toeplitz(c,r)
beta <- mldivide(X, y[1:400])
yhat = X %*% beta
plot(y[1:400])
lines(yhat[1:400], col="red")
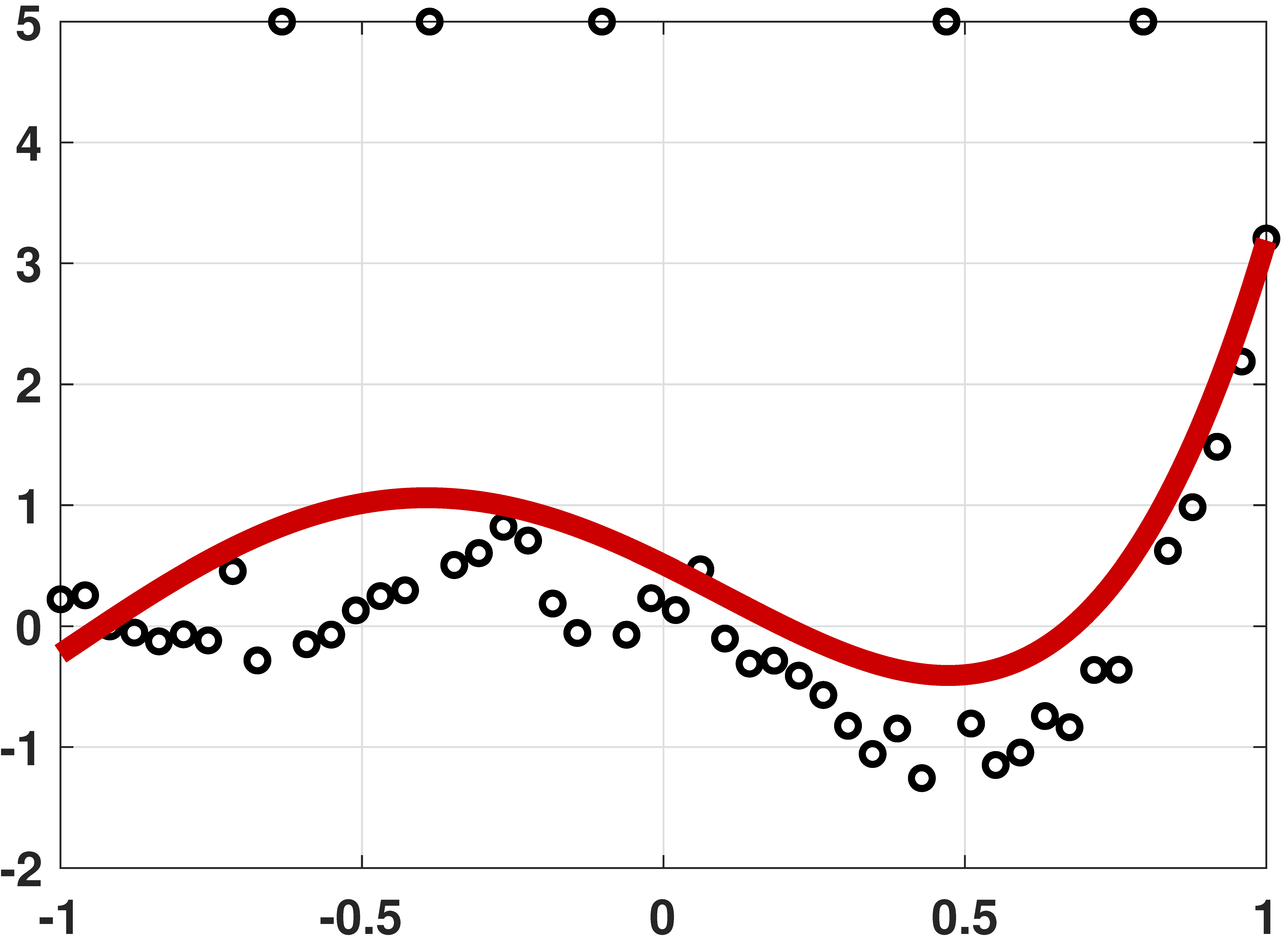
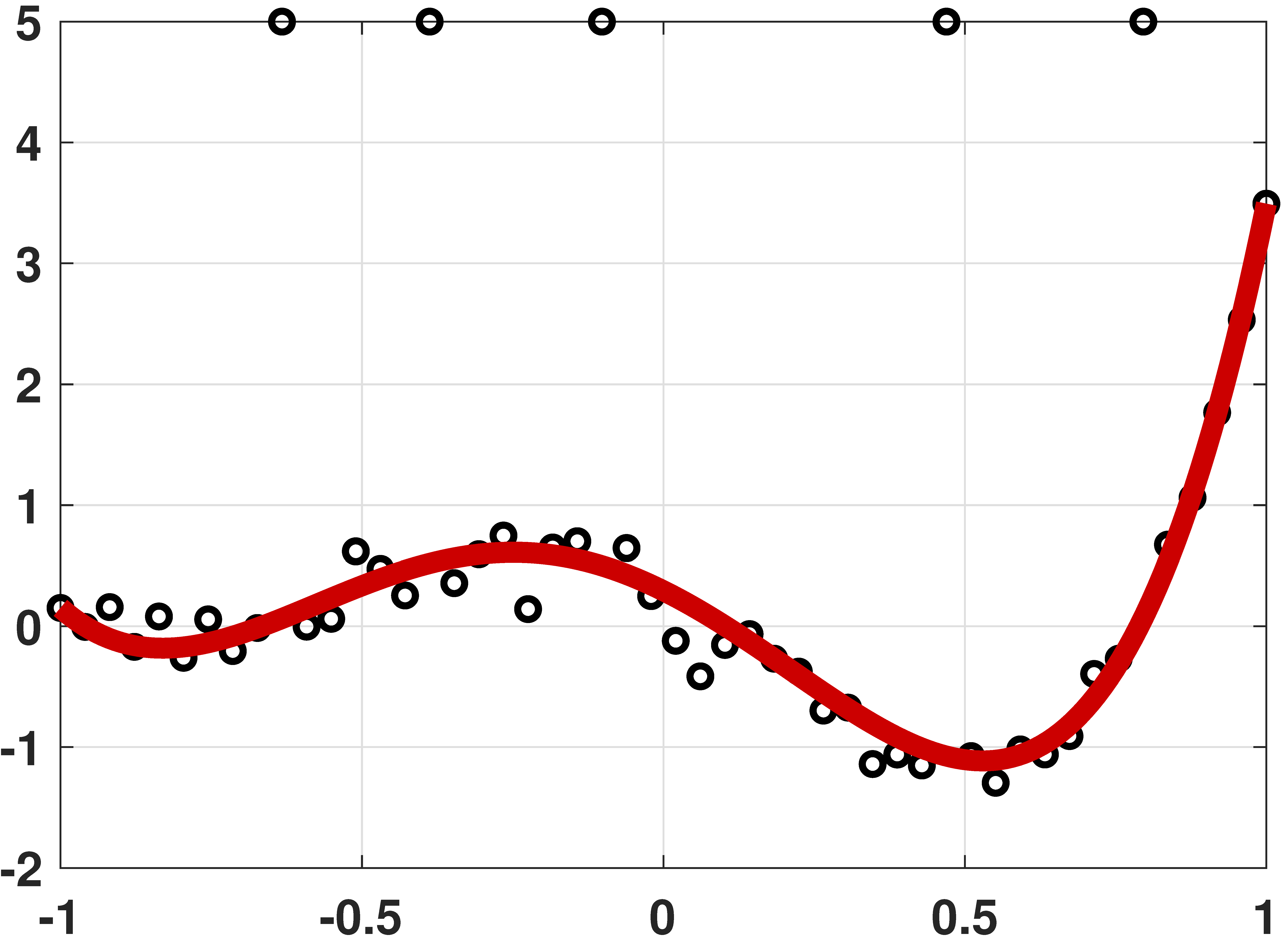
Robust regression by linear programming
% MATLAB code to demonstrate robust regression
N = 50;
x = linspace(-1,1,N)';
a = [-0.001 0.01 0.55 1.5 1.2];
y = a(1)*legendreP(0,x) + a(2)*legendreP(1,x) + ...
a(3)*legendreP(2,x) + a(4)*legendreP(3,x) + ...
a(5)*legendreP(4,x) + 0.2*randn(N,1);
idx = [10, 16, 23, 37, 45];
y(idx) = 5;
X = [x(:).^0 x(:).^1 x(:).^2 x(:).^3 x(:).^4];
A = [X -eye(N); -X -eye(N)];
b = [y(:); -y(:)];
c = [zeros(1,5) ones(1,N)]';
theta = linprog(c, A, b);
t = linspace(-1,1,200)';
yhat = theta(1) + theta(2)*t(:) + ...
theta(3)*t(:).^2 + theta(4)*t(:).^3 + ...
theta(5)*t(:).^4;
plot(x,y, 'ko','LineWidth',2); hold on;
plot(t,yhat,'r','LineWidth',4);
# Python code to demonstrate robust regression
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import eval_legendre
from scipy.optimize import linprog
N = 50
x = np.linspace(-1,1,N)
a = np.array([-0.001, 0.01, 0.55, 1.5, 1.2])
y = a[0]*eval_legendre(0,x) + a[1]*eval_legendre(1,x) + \
a[2]*eval_legendre(2,x) + a[3]*eval_legendre(3,x) + \
a[4]*eval_legendre(4,x) + 0.2*np.random.randn(N)
idx = [10,16,23,37,45]
y[idx] = 5
X = np.column_stack((np.ones(N), x, x**2, x**3, x**4))
A = np.vstack((np.hstack((X, -np.eye(N))), np.hstack((-X, -np.eye(N)))))
b = np.hstack((y,-y))
c = np.hstack((np.zeros(5), np.ones(N)))
res = linprog(c, A, b, bounds=(None,None), method="revised simplex")
theta = res.x
t = np.linspace(-1,1,200)
yhat = theta[0]*np.ones(200) + theta[1]*t + theta[2]*t**2 + \
theta[3]*t**3 + theta[4]*t**4
plt.plot(x,y,'o',markersize=12)
plt.plot(t,yhat, linewidth=8)
plt.show()
# Julia code to demonstrate robust regression using LinearAlgebra, LegendrePolynomials, Convex, SCS import MathOptInterface const MOI = MathOptInterface #---------------------------------------------------------- """ linprog_Convex(c,A,sense,b) A wrapper for doing linear programming with Convex.jl/SCS.jl. It solves, for instance, `c'x` st. `A*x<=b` """ function linprog_Convex(c,A,sense,b) n = length(c) x = Variable(n) #c1 = sense(A*x,b) #restriction, for Ax <= b, use sense = (<=) c1 = A*x <= b prob = minimize(dot(c,x),c1) solve!(prob,()->SCS.Optimizer(verbose = false)) x_i = prob.status == MOI.OPTIMAL ? vec(evaluate(x)) : NaN return x_i end #---------------------------------------------------------- N = 50 x = range(-1,stop=1,length=N) a = [-0.001, 0.01, 0.55, 1.5, 1.2] y = hcat([Pl.(x,p) for p=0:4]...)*a + 0.05*randn(N) # generate data idx = [10, 16, 23, 37, 45] y[idx] .= 5 X = x.^[0 1 2 3 4] A = [X -I; -X -I] b = [y; -y] c = [zeros(5);ones(N)] theta = linprog_Convex(c,A,(<=),b) t = range(-1,stop=1,length=200) yhat = (t.^[0 1 2 3 4])*theta[1:5] p5 = scatter(x,y,makershape=:circle,label="data",legend=:bottomleft) plot!(t,yhat,linecolor=:red,linewidth=4,label="fitted curve") display(p5)
# R code to demonstrate robust regression
library(pracma)
N <- 50
x <- linspace(-1,1,N)
a <- c(-0.001, 0.01, 0.55, 1.5, 1.2)
y <- a[1]*legendre(0, x) + a[2]*legendre(1, x)[1,] +
a[3]*legendre(2, x)[1,] + a[4]*legendre(3, x)[1,] +
a[5]*legendre(4, x)[1,] + 0.2*rnorm(N)
idx <- c(10, 16, 23, 37, 45)
y[idx] <- 5
X <- cbind(rep(1,N), x, x**2, x**3, x**4)
A <- rbind(cbind(X, -1*diag(N)), cbind(-X, -1*diag(N)))
b <- c(y, -y)
c <- c(rep(0, 5), rep(1, N))
res <- linprog(c, A, b, maxiter=1000000)
beta <- res.x
t <- linspace(-1, 1, 200)
Chapter 7.2 Overfitting
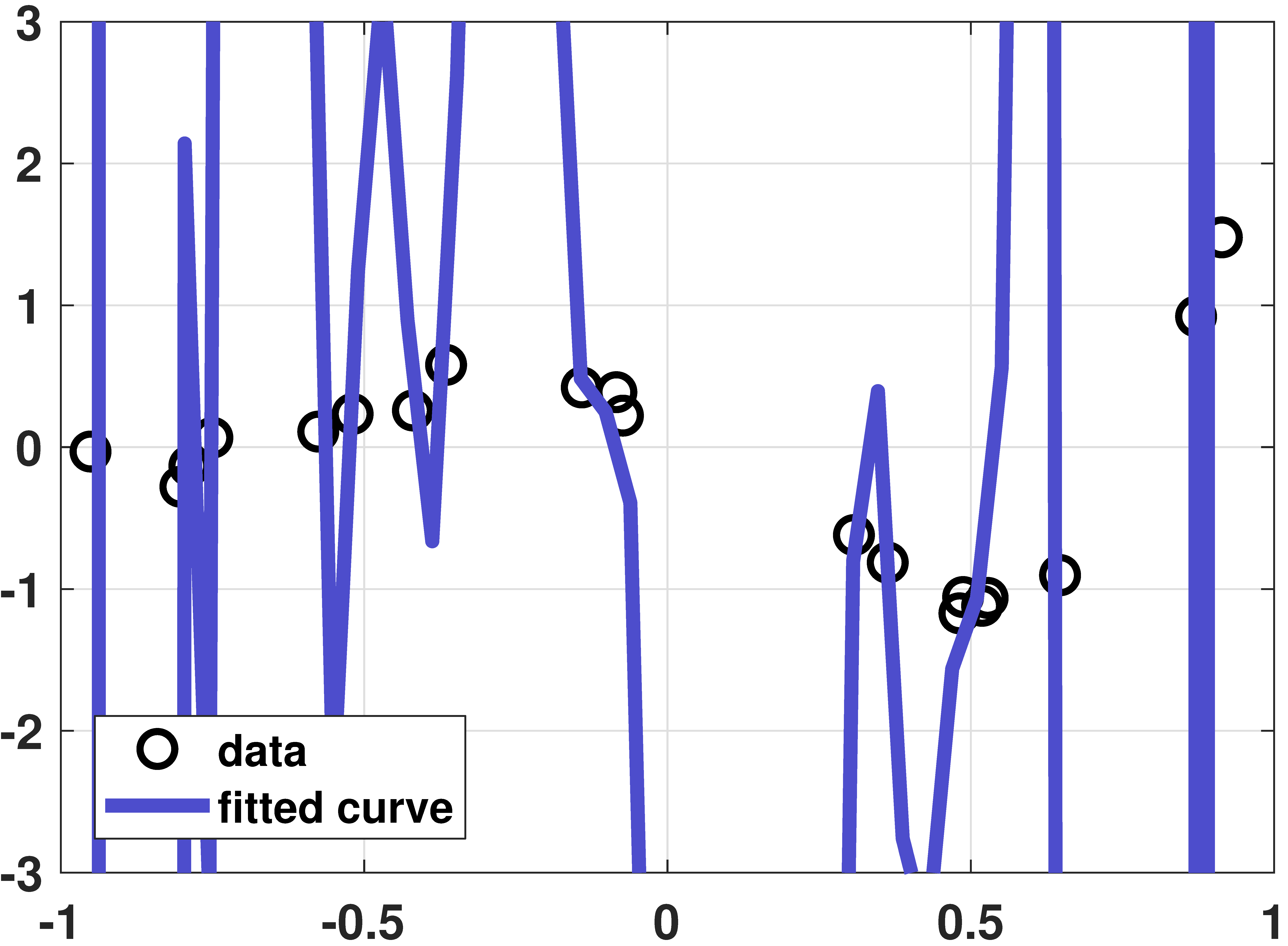
Overfitting example
% MATLAB: An overfitting example
N = 20;
x = sort(1*(rand(N,1)*2-1));
a = [-0.001 0.01 +0.55 1.5 1.2];
y = a(1)*legendreP(0,x) + a(2)*legendreP(1,x) + ...
a(3)*legendreP(2,x) + a(4)*legendreP(3,x) + ...
a(5)*legendreP(4,x) + 0.1*randn(N,1);
figure(1);
P = 20;
X = zeros(N, P+1);
for p=0:P
tmp = legendreP(p,x);
X(:,p+1) = tmp(:);
end
beta = X\y;
t = linspace(-1, 1, 50);
Xhat = zeros(length(t), P+1);
for p=0:P
tmp = legendreP(p,t);
Xhat(:,p+1) = tmp(:);
end
yhat = Xhat*beta;
plot(x,y, 'ko','LineWidth',2, 'MarkerSize', 10); hold on;
plot(t,yhat,'LineWidth',4,'Color',[0.3 0.3 0.8]);
legend('data', 'fitted curve','Location','SW');
grid on;
set(gcf, 'Position', [100, 100, 600, 400]);
set(gca,'FontWeight','bold','fontsize',14);
axis([-1 1 -3 3]);
# Julia: An overfitting example
using LegendrePolynomials
N = 20
x = sort(rand(N)*2 .- 1)
a = [-0.001, 0.01, 0.55, 1.5, 1.2]
y = hcat([Pl.(x,p) for p=0:4]...)*a + 0.1*randn(N)
P = 20
X = hcat([Pl.(x,p) for p=0:P]...)
beta = X\y
t = range(-1,stop=1,length=50)
Xhat = hcat([Pl.(t,p) for p=0:P]...)
yhat = Xhat*beta
p6 = scatter(x,y,makershape=:circle,label="data",legend=:bottomleft,ylims = (-3,3))
plot!(t,yhat,linecolor=:blue,linewidth=4,label="fitted curve")
display(p6)
# R: An overfitting example
N = 20
x = sort(rnorm(N)*2-1)
a = c(-0.001, 0.01, 0.55, 1.5, 1.2)
y = a[1]*legendre(0, x) + a[2]*legendre(1, x)[1,] +
a[3]*legendre(2, x)[1,] + a[4]*legendre(3, x)[1,] +
a[5]*legendre(4, x)[1,] + 0.1*rnorm(N)
P = 20
X = matrix(0, N, P+1)
for (p in 0:P) {
tmp = matrix(legendre(p, x))[1,]
X[,p+1] = tmp
}
beta = mldivide(X, y)
t = linspace(-1, 1, 50)
Xhat = matrix(0, length(t), P+1)
for (p in 0:P) {
tmp = matrix(legendre(p, t))[1,]
Xhat[,p+1] = tmp
}
yhat = mldivide(Xhat, beta)
plot(x, y)
lines(t, yhat)
Learning curve
% MATLAB
Nset = round(logspace(1,3,20));
E_train = zeros(1,length(Nset));
E_test = zeros(1,length(Nset));
a = [1.3, 2.5];
for j = 1:length(Nset)
N = Nset(j);
x = linspace(-1,1,N)';
E_train_temp = zeros(1,1000);
E_test_temp = zeros(1,1000);
X = [ones(N,1), x(:)];
for i = 1:1000
y = a(1) + a(2)*x + randn(size(x));
y1 = a(1) + a(2)*x + randn(size(x));
theta = X\y(:);
yhat = theta(1) + theta(2)*x;
E_train_temp(i) = mean((yhat(:)-y(:)).^2);
E_test_temp(i) = mean((yhat(:)-y1(:)).^2);
end
E_train(j) = mean(E_train_temp);
E_test(j) = mean(E_test_temp);
end
semilogx(Nset, E_train, 'kx', 'LineWidth', 2, 'MarkerSize', 16); hold on;
semilogx(Nset, E_test, 'ro', 'LineWidth', 2, 'MarkerSize', 8);
semilogx(Nset, 1-2./Nset, 'k', 'LineWidth', 4);
semilogx(Nset, 1+2./Nset, 'r', 'LineWidth', 4);
# Python
import numpy as np
import matplotlib.pyplot as plt
Nset = np.logspace(1,3,20)
Nset = Nset.astype(int)
E_train = np.zeros(len(Nset))
E_test = np.zeros(len(Nset))
for j in range(len(Nset)):
N = Nset[j]
x = np.linspace(-1,1,N)
a = np.array([1, 2])
E_train_tmp = np.zeros(1000)
E_test_tmp = np.zeros(1000)
for i in range(1000):
y = a[0] + a[1]*x + np.random.randn(N)
X = np.column_stack((np.ones(N), x))
theta = np.linalg.lstsq(X, y, rcond=None)[0]
yhat = theta[0] + theta[1]*x
E_train_tmp[i] = np.mean((yhat-y)**2)
y1 = a[0] + a[1]*x + np.random.randn(N)
E_test_tmp[i] = np.mean((yhat-y1)**2)
E_train[j] = np.mean(E_train_tmp)
E_test[j] = np.mean(E_test_tmp)
plt.semilogx(Nset, E_train, 'kx')
plt.semilogx(Nset, E_test, 'ro')
plt.semilogx(Nset, (1-2/Nset), linewidth=4, c='k')
plt.semilogx(Nset, (1+2/Nset), linewidth=4, c='r')
# Julia using Statistics Nset = round.( Int,exp10.(range(1,stop=3,length=20)) ) #10,13,16,21,... E_train = zeros(length(Nset)) E_test = zeros(length(Nset)) a = [1.3, 2.5] for j = 1:length(Nset) local N,x,E_train_temp,E_test_temp,X N = Nset[j] x = range(-1,stop=1,length=N) E_train_temp = zeros(1000) E_test_temp = zeros(1000) X = [ones(N) x] for i = 1:1000 local y,y1,theta,yhat y = a[1] .+ a[2]*x + randn(N) y1 = a[1] .+ a[2]*x + randn(N) theta = X\y yhat = theta[1] .+ theta[2]*x E_train_temp[i] = mean(abs2,yhat-y) E_test_temp[i] = mean(abs2,yhat-y1) end E_train[j] = mean(E_train_temp) E_test[j] = mean(E_test_temp) end p7 = scatter(Nset,E_train,xscale=:log10,markershape=:x,markercolor=:black,label="Training Error") scatter!(Nset,E_test,xscale=:log10,markershape=:circle,markercolor=:red,label="Testing Error") plot!(Nset,1.0 .- 2.0./Nset,xscale=:log10,linestyle=:solid,color=:black,label="") plot!(Nset,1.0 .+ 2.0./Nset,xscale=:log10,linestyle=:solid,color=:red,label="") display(p7)
Chapter 7.3 Bias and Variance
Mean estimator
% MATLAB code to visualize the average predictor
N = 20;
a = [5.7, 3.7, -3.6, -2.3, 0.05];
x = linspace(-1,1,N);
yhat = zeros(100,50);
for i=1:100
X = [x(:).^0, x(:).^1, x(:).^2, x(:).^3, x(:).^4];
y = X*a(:) + 0.5*randn(N,1);
theta = X\y(:);
t = linspace(-1, 1, 50);
yhat(i,:) = theta(1) + theta(2)*t(:) + theta(3)*t(:).^2 ...
+ theta(4)*t(:)^3 + theta(5)*t(:).^4;
end
figure;
plot(t, yhat, 'color', [0.6 0.6 0.6]); hold on;
plot(t, mean(yhat), 'LineWidth', 4, 'color', [0.8 0 0]);
axis([-1 1 -2 2]);
# Python code to visualize the average predictor
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import eval_legendre
np.set_printoptions(precision=2, suppress=True)
N = 20
x = np.linspace(-1,1,N)
a = np.array([0.5, -2, -3, 4, 6])
yhat = np.zeros((50,100))
for i in range(100):
y = a[0] + a[1]*x + a[2]*x**2 + \
a[3]*x**3 + a[4]*x**4 + 0.5*np.random.randn(N)
X = np.column_stack((np.ones(N), x, x**2, x**3, x**4))
theta = np.linalg.lstsq(X, y, rcond=None)[0]
t = np.linspace(-1,1,50)
Xhat = np.column_stack((np.ones(50), t, t**2, t**3, t**4))
yhat[:,i] = np.dot(Xhat, theta)
plt.plot(t, yhat[:,i], c='gray')
plt.plot(t, np.mean(yhat, axis=1), c='r', linewidth=4)
# Julia code to visualize the average predictor N = 20 a = [5.7, 3.7, -3.6, -2.3, 0.05] x = range(-1,stop=1,length=N) X = x.^[0 1 2 3 4] t = range(-1,stop=1,length=50) tMat = t.^[0 1 2 3 4] yhat = zeros(50,100) #50x100 instead of 100x50 for i = 1:100 local y,theta y = X*a + 0.5*randn(N) theta = X\y yhat[:,i] = tMat*theta end p8 = plot(t,yhat,linecolor=:gray,label="") plot!(t,mean(yhat,dims=2),linecolor=:red,linewidth=4,label="") display(p8)
# R code to visualize the average predictor
library(pracma)
N = 20
x = linspace(-1,1,N)
a = c(0.5, -2, -3, 4, 6)
yhat = matrix(0,50,100)
plot(NULL, xlim=c(-1,1), ylim=c(-3,3))
for (i in 1:100) {
y = a[1] + a[2]*x + a[3]*x**2 + a[4]*x**3 + a[5]*x**4 + 0.5*rnorm(N)
X = cbind(rep(1,N), x, x**2, x**3, x**4)
theta = lsfit(X, y)$coefficients[2:6]
t = linspace(-1, 1, 50)
Xhat = cbind(rep(1, N), t, t**2, t**3, t**4)
yhat[,i] = Xhat %*% theta
lines(t, yhat[,i], col="gray")
}
lines(t, rowMeans(yhat), col="red", lwd=5)
Chapter 7.4 Regularization
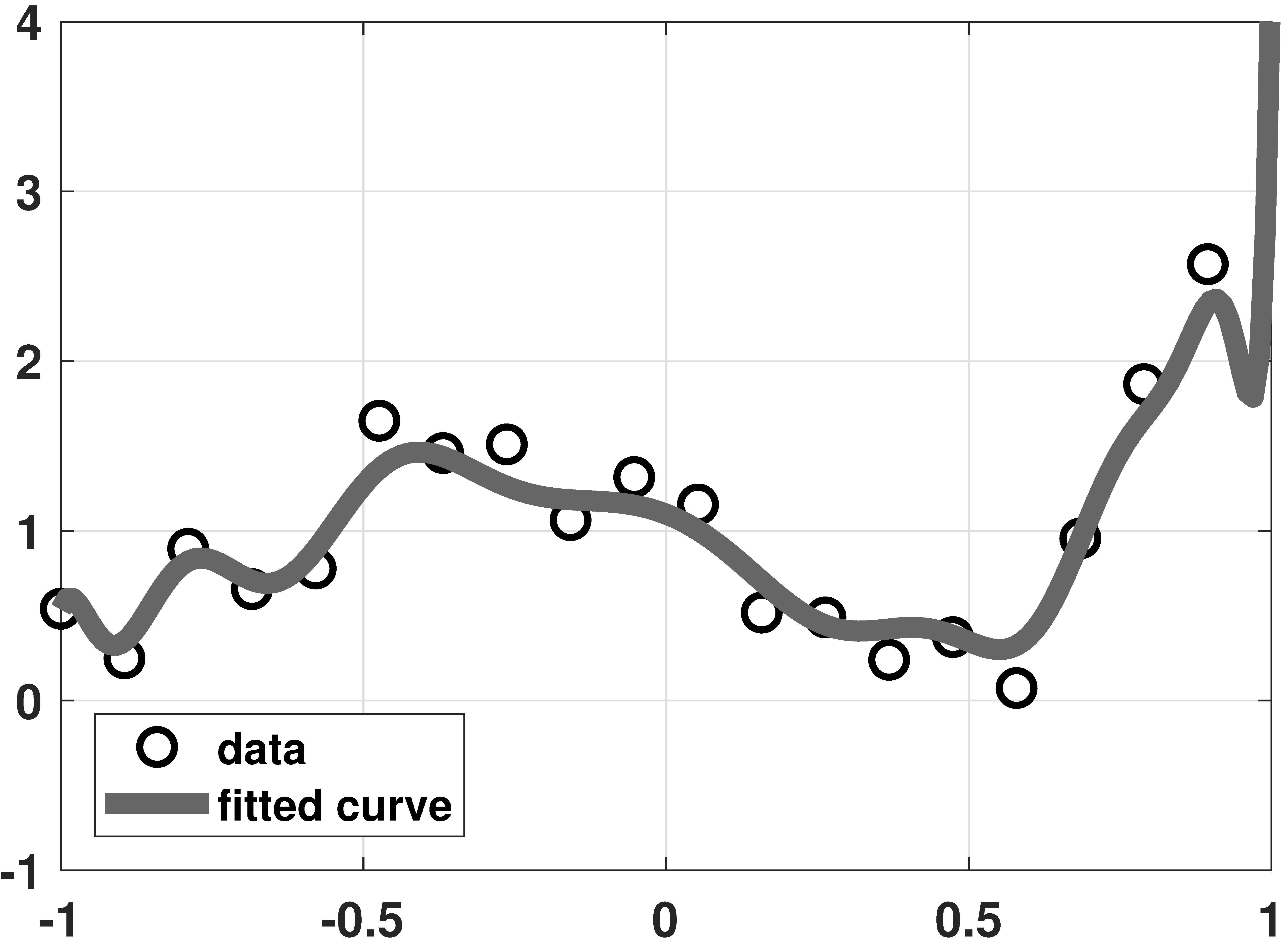
Ridge regression
% MATLAB code to demonstrate a ridge regression example
% Generate data
N = 20;
x = linspace(-1,1,N);
a = [0.5, -2, -3, 4, 6];
y = a(1)+a(2)*x(:)+a(3)*x(:).^2+a(4)*x(:).^3+a(5)*x(:).^4+0.25*randn(N,1);
% Ridge regression
lambda = 0.1;
d = 20;
X = zeros(N, d);
for p=0:d-1
X(:,p+1) = x(:).^p;
end
A = [X; sqrt(lambda)*eye(d)];
b = [y(:); zeros(d,1)];
theta = A\b;
% Interpolate and display results
t = linspace(-1, 1, 500);
Xhat = zeros(length(t), d);
for p=0:d-1
Xhat(:,p+1) = t(:).^p;
end
yhat = Xhat*theta;
plot(x,y, 'ko','LineWidth',2, 'MarkerSize', 10); hold on;
plot(t,yhat,'LineWidth',4,'Color',[0.2 0.2 0.9]);
# Python code to demonstrate a ridge regression example
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import eval_legendre
np.set_printoptions(precision=2, suppress=True)
N = 20
x = np.linspace(-1,1,N)
a = np.array([0.5, -2, -3, 4, 6])
y = a[0] + a[1]*x + a[2]*x**2 + \
a[3]*x**3 + a[4]*x**4 + 0.2*np.random.randn(N)
d = 20
X = np.zeros((N, d))
for p in range(d):
X[:,p] = x**p
lambd = 0.1
A = np.vstack((X, np.sqrt(lambd)*np.eye(d)))
b = np.hstack((y, np.zeros(d)))
theta = np.linalg.lstsq(A, b, rcond=None)[0]
t = np.linspace(-1, 1, 500)
Xhat = np.zeros((500,d))
for p in range(d):
Xhat[:,p] = t**p
yhat = np.dot(Xhat, theta)
plt.plot(x,y,'o',markersize=12)
plt.plot(t,yhat, linewidth=4)
plt.show()
# Julia code to demonstrate a ridge regression example #---------------------------------------------------------- """ RidgeRegression(Y,X,lambda,beta0=0) Calculate ridge regression estimate with targetr vector beta₀. """ function RidgeRegression(Y,X,lambda,beta0=0) K = size(X,2) isa(beta0,Number) && (beta0=fill(beta0,K)) b = (X'X+lambda*I)\(X'Y+lambda*beta0) #same as inv(X'X+lambda*I)*(X'Y+lambda*beta0) return b end #---------------------------------------------------------- N = 20 # Generate data x = range(-1,stop=1,length=N) a = [0.5, -2, -3, 4, 6] y = x.^[0 1 2 3 4]*a + 0.25*randn(N) lambda = 0.1 # Ridge regression d = 20 X = x.^collect(0:d-1)' A = [X; sqrt(lambda)I] b = [y; zeros(d)] theta = A\b theta_alt = RidgeRegression(y,X,lambda) # alternative ridge regression display([theta theta_alt]) t = range(-1,stop=1,length=500) Xhat = t.^collect(0:d-1)' yhat = Xhat*theta p9 = scatter(x,y,makershape=:circle,label="data",legend=:bottomleft) plot!(t,yhat,linecolor=:blue,linewidth=4,label="fitted curve") display(p9)
# R code to demonstrate a ridge regression example
N = 20
x = linspace(-1,1,N)
a = c(0.5, -2, -3, 4, 6)
y = a[1] + a[2]*x + a[3]*x**2 + a[4]*x**3 + a[5]*x**4 + 0.2*rnorm(N)
d = 20
X = matrix(0, N, d)
for (p in 1:d) {
X[,p] = x**p
}
lambd = 0.1
A = rbind(X, (lambd)*diag(d)**(1/2))
b = c(y, rep(0, d))
theta = lsfit(A, b)$coefficients[2:21]
t = linspace(-1, 1, 500)
Xhat = matrix(0, 500,d)
for (p in 1:d) {
Xhat[,p] = t**p
}
yhat = Xhat %*% theta
plot(x, y)
grid()
lines(t, yhat, col="darkgray", lwd=4)
legend("bottomleft", c("Data", "Fitted curve"), pch=c(1, NA), lty=c(NA, 1))
LASSO regression
Data download: ch7_data_crime.txt (1KB)
% MATLAB
data = load('./dataset/ch7_data_crime.txt');
y = data(:,1); % The observed crime rate
X = data(:,3:end); % Feature vectors
[N,d]= size(X);
lambdaset = logspace(-1,8,50);
theta_store = zeros(d,50);
for i=1:length(lambdaset)
lambda = lambdaset(i);
cvx_begin
variable theta(d)
minimize( sum_square(X*theta-y) + lambda*norm(theta,1) )
% minimize( sum_square(X*theta-y) + lambda*sum_square(theta) )
cvx_end
theta_store(:,i) = theta(:);
end
figure(1);
semilogx(lambdaset, theta_store, 'LineWidth', 4);
legend('funding','% high', '% no high', '% college', ...
'% graduate', 'Location','NW');
xlabel('lambda');
ylabel('feature attribute');
# Python import cvxpy as cvx import numpy as np import matplotlib.pyplot as plt data = np.loadtxt("/content/ch7_data_crime.txt") y = data[:,0] X = data[:,2:7] N,d = X.shape lambd_set = np.logspace(-1,8,50) theta_store = np.zeros((d,50)) for i in range(50): lambd = lambd_set[i] theta = cvx.Variable(d) objective = cvx.Minimize( cvx.sum_squares(X*theta-y) \ + lambd*cvx.norm1(theta) ) # objective = cvx.Minimize( cvx.sum_squares(X*theta-y) \ + lambd*cvx.sum_squares(theta) ) prob = cvx.Problem(objective) prob.solve() theta_store[:,i] = theta.value for i in range(d): plt.semilogx(lambd_set, theta_store[i,:])
# Julia """ LassoEN(Y,X,lambda,δ,beta₀) Do Lasso (set lambda>0,δ=0), ridge (set lambda=0,δ>0) or elastic net regression (set lambda>0,δ>0). Setting beta₀ allows us to specify the target level. """ function LassoEN(Y,X,lambda,δ=0.0,beta₀=0) K = size(X,2) isa(beta₀,Number) && (beta₀=fill(beta₀,K)) #b_ls = X\Y #LS estimate of weights, no restrictions Q = X'X c = X'Y #c'b = Y'X*b b = Variable(K) #define variables to optimize over L1 = quadform(b,Q) #b'Q*b L2 = dot(c,b) #c'b L3 = norm(b-beta₀,1) #sum(|b-beta₀|) L4 = sumsquares(b-beta₀) #sum((b-beta₀)^2) Sol = minimize(L1-2*L2+lambda*L3+δ*L4) #u'u + lambda*sum(|b|) + δ*sum(b^2), where u = Y-Xb solve!(Sol,()->SCS.Optimizer(verbose = false)) b_i = vec(evaluate(b)) return b_i end #---------------------------------------------------------- using LinearAlgebra, DelimitedFiles, Convex, SCS import MathOptInterface const MOI = MathOptInterface data = readdlm("dataset/ch7_data_crime.txt") y = data[:,1] # the observed crime rate X = data[:,3:end] # feature vectors (N,d) = size(X) (y,X) = (y.-mean(y),X.-mean(X,dims=1)) # de-meaning all variables lambdaset = exp10.(range(-2,stop=4,length=50)) # adjusted range of lambda values since X/100 is used (theta_store,theta_store2,theta_store3) = [zeros(50,d) for _=1:3] # 50 x d instead of d x 50 for i = 1:length(lambdaset) theta_store[i,:] = LassoEN(y/100,X/100,lambdaset[i]) # LASSO, /100 improves the numerical stability theta_store2[i,:] = LassoEN(y/100,X/100,0,lambdaset[i]) # ridge regression #theta_store3[i,:] = RidgeRegression(y/100,X/100,lambdaset[i]) # alternative ridge regression end #display(theta_store2-theta_store3) # compare solutions p10 = plot(lambdaset,theta_store,xscale=:log10,title="LASSO",xlabel="lambda",ylabel="feature attribute", label = ["funding" "% high" "% no high" "% college" "% graduate"], linecolor = [:blue :red :yellow3 :magenta :green],ylims=(-5,15)) display(p10) p10b = plot(lambdaset,theta_store2,xscale=:log10,title="ridge regression",xlabel="lambda",ylabel="feature attribute", label = ["funding" "% high" "% no high" "% college" "% graduate"], linecolor = [:blue :red :yellow3 :magenta :green],ylims=(-5,15)) display(p10b)
# R library(pracma) library(CVXR) data = scan("ch7_data_crime.txt") data = matrix(data, nrow=7) data = t(data) y = data[,1] X = data[,3:8] N = dim(X)[0] d = dim(X)[1] lambd_set = logspace(-1,8,50) theta_store = matrix(0, d,50) for (i in 1:50) { lambd = lambd_set[i] theta = Variable(d) lambd = lambd_set[i] objective = Minimize(sum_squares(X %*% theta-y) + lambd*norm1(theta)) # objective = cvx.Minimize( cvx.sum_squares(X*theta-y) \ prob = Problem(objective) result = solve(prob) theta_store[,i] = result$getValue(theta) } plot(NULL, xlim=c(10**(-2), 10**8), ylim=c(-2,14)) for (i in 1:d) { lines(log(lambd_set), theta_store[i,]) }
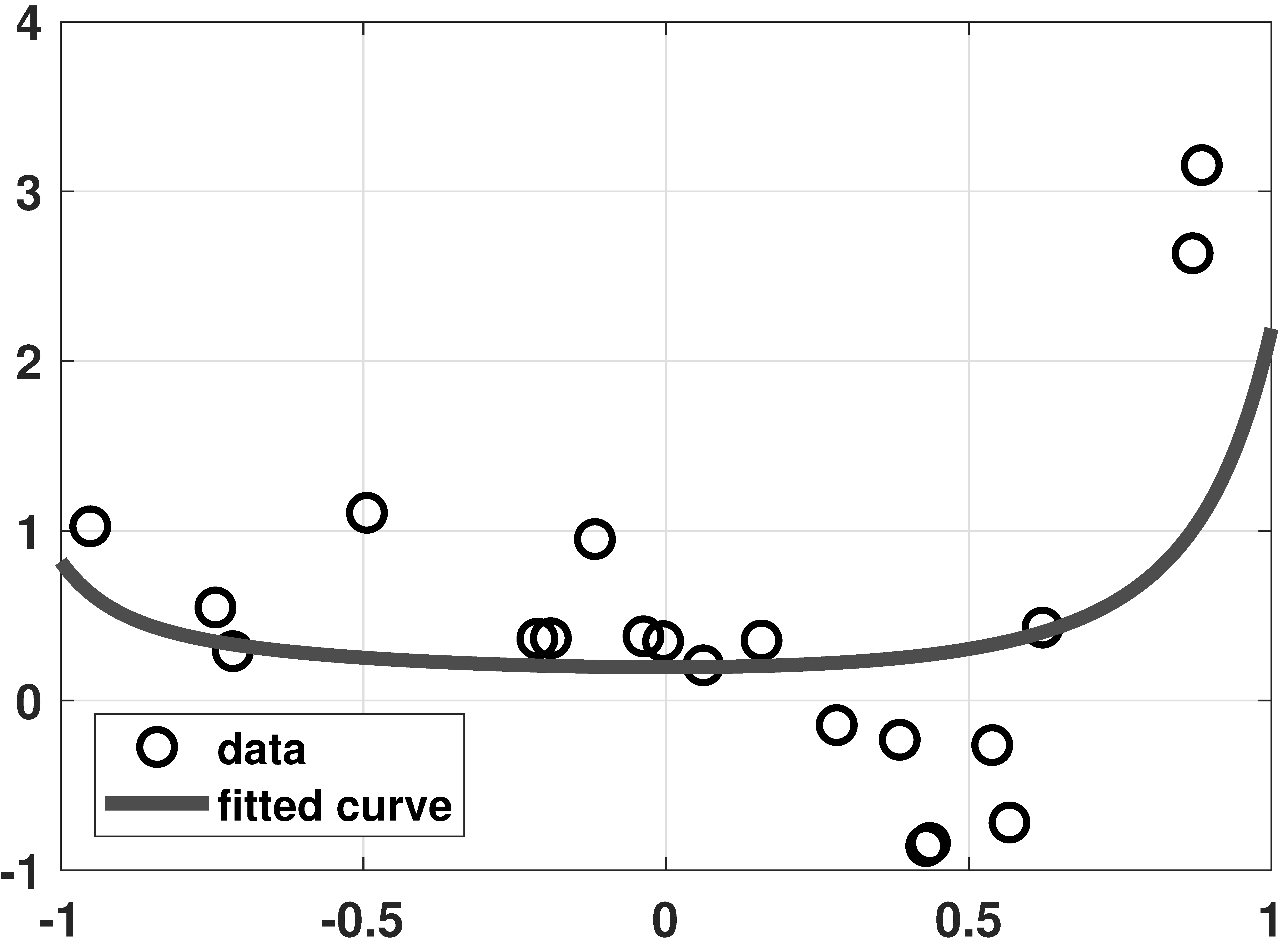
LASSO vs Ridge
% MATLAB code to demonstrate overfitting and LASSO
% Generate data
N = 20;
x = linspace(-1,1,N)';
a = [1, 0.5, 0.5, 1.5, 1];
y = a(1)*legendreP(0,x)+a(2)*legendreP(1,x)+a(3)*legendreP(2,x)+ ...
a(4)*legendreP(3,x)+a(5)*legendreP(4,x)+0.25*randn(N,1);
% Solve LASSO using CVX
d = 20;
X = zeros(N, d);
for p=0:d-1
X(:,p+1) = reshape(legendreP(p,x),N,1);
end
lambda = 2;
cvx_begin
variable theta(d)
minimize( sum_square( X*theta - y ) + lambda * norm(theta , 1) )
cvx_end
% Plot results
t = linspace(-1, 1, 200);
Xhat = zeros(length(t), d);
for p=0:d-1
Xhat(:,p+1) = reshape(legendreP(p,t),200,1);
end
yhat = Xhat*theta;
plot(x,y, 'ko','LineWidth',2, 'MarkerSize', 10); hold on;
plot(t,yhat,'LineWidth',6,'Color',[0.2 0.5 0.2]);
# Python code to demonstrate overfitting and LASSO import cvxpy as cvx import numpy as np import matplotlib.pyplot as plt # Setup the problem N = 20 x = np.linspace(-1,1,N) a = np.array([1, 0.5, 0.5, 1.5, 1]) y = a[0]*eval_legendre(0,x) + a[1]*eval_legendre(1,x) + \ a[2]*eval_legendre(2,x) + a[3]*eval_legendre(3,x) + \ a[4]*eval_legendre(4,x) + 0.25*np.random.randn(N) # Solve LASSO using CVX d = 20 lambd = 1 X = np.zeros((N, d)) for p in range(d): X[:,p] = eval_legendre(p,x) theta = cvx.Variable(d) objective = cvx.Minimize( cvx.sum_squares(X*theta-y) \ + lambd*cvx.norm1(theta) ) prob = cvx.Problem(objective) prob.solve() thetahat = theta.value # Plot the curves t = np.linspace(-1, 1, 500) Xhat = np.zeros((500,d)) for p in range(P): Xhat[:,p] = eval_legendre(p,t) yhat = np.dot(Xhat, thetahat) plt.plot(x, y, 'o') plt.plot(t, yhat, linewidth=4)
# Julia code to demonstrate overfitting and LASSO using LinearAlgebra, LegendrePolynomials, Convex, SCS import MathOptInterface const MOI = MathOptInterface N = 20 # Generate data x = range(-1,stop=1,length=N) a = [1, 0.5, 0.5, 1.5, 1] y = hcat([Pl.(x,p) for p=0:4]...)*a + 0.25*randn(N) d = 20 # Solve LASSO using Convex.jl X = hcat([Pl.(x,p) for p=0:d-1]...) lambda = 2 theta = LassoEN(y,X,lambda) t = range(-1,stop=1,length=200) Xhat = hcat([Pl.(t,p) for p=0:d-1]...) yhat = Xhat*theta p11 = scatter(x,y,makershape=:circle,label="data",legend=:bottomleft) plot!(t,yhat,linecolor=:blue,linewidth=4,label="fitted curve") display(p11)
# R code to demonstrate overfitting and LASSO # Setup the problem install.packages("CVXR") library(pracma) library(CVXR) N = 20 x = linspace(-1,1,N) a = c(1, 0.5, 0.5, 1.5, 1) y = a[1]*legendre(0,x) + a[2]*legendre(1,x)[1,] + a[3]*legendre(2,x)[1,] + a[4]*legendre(3,x)[1,] + a[5]*legendre(4,x)[1,] + 0.25*rnorm(N) # Solve LASSO using CVX d = 20 lambd = 1 X = matrix(0, N, d) for (p in 1:d) { X[,p] = legendre(p,x)[1,] } theta = Variable(d) objective = Minimize(sum_squares(X %*% theta-y) + lambd*norm1(theta)) prob = Problem(objective) result = solve(prob) thetahat = result$getValue(theta) # Plot the curves t = linspace(-1, 1, 500) Xhat = matrix(0, 500, d) for (p in 1:P) { Xhat[,p] = legendre(p,t)[1,] } yhat = Xhat %*% thetahat plot(x, y) lines(t, yhat)